---

Volatility Timing Portfolio and Risk Management

---

Volatility Timing

Volatility timing is an investment strategy that aims to adjust the exposure of a portfolio based on the volatility of the market. The goal of this strategy is to lower exposure to risky assets when the volatility of recent returns for those assets is relatively high and raise exposure when the volatility is low. The idea behind volatility timing is that high volatility is associated with increased risk, and therefore, it is better to reduce exposure to risky assets during periods of high volatility to avoid losses. Conversely, low volatility is associated with lower risk, and therefore, it is better to increase exposure to risky assets during periods of low volatility to maximize returns. To understand volatility timing, we need to define some mathematical concepts. In finance, volatility is a measure of the degree of variation of a financial instrument's price over time. It is usually calculated as the standard deviation of the instrument's returns over a certain period. The formula for calculating the standard deviation is:
\[\sigma = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n-1}}\]
where \(\sigma\) is the standard deviation, \(x_i\) is the return for period \(i\) , \(\mu\) is the mean return, and \(n\) is the number of periods.
The Sharpe ratio is a measure of risk-adjusted return that takes into account the volatility of the investment. It is calculated as the excess return of the investment over the risk-free rate divided by the standard deviation of the investment's returns. The formula for calculating the Sharpe ratio is:
\[Sharpe\ ratio = \frac{R_p - R_f}{\sigma_p}\]
where \(R_p\) is the return of the investment, \(R_f\) is the risk-free rate, and \(\sigma_p\) is the standard deviation of the investment's returns. To implement volatility timing, we need to calculate the active return of the stock. The active return is the return of the stock adjusted for the volatility of the market. The formula for calculating the active return is:
\[Active\ return = \frac{c}{\sigma_{t-1}^2} \times R_t\]
where \(c\) is a constant,\(\sigma_{t-1}\) is the standard deviation of the market returns in the previous period, and \(R_t\) is the return of the stock in the current period. Once we have calculated the active return, we need to standardize it by dividing it by the standard deviation of the monthly returns. The formula for standardizing the active return is:
\[Standardized\ active\ return = Active\ return \times \frac{\sigma_{passive\ returns}}{\sigma_{active\ returns} }\]
The following Python code implements the method for the NASDAQ Composite index:

import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings(action='ignore')
import yfinance as yf
import matplotlib.pyplot as plt

daily = pd.DataFrame()
daily['Close'] = yf.download('^IXIC')['Close']
daily['Return'] = np.log(daily['Close'] / daily['Close'].shift())
daily
monthly = pd.DataFrame(columns=['date', 'return', 'volatility'])

returns = []
for i in range(1, len(daily)-2):
    today = daily.index[i].month
    tomorrow = daily.index[i+1].month    
    if today == tomorrow:
        returns.append(daily['Return'].iloc[i])
    else:
        returns.append(daily['Return'].iloc[i])
        monthly.loc[len(monthly)] = [daily.index[i], np.sum(returns), np.std(returns)]
        
        returns=[]

c = 1. 
monthly['active'] = c / monthly['volatility'].shift() ** 2 * monthly['return']
monthly['active'] = monthly['return'].std() / monthly['active'].std() * monthly['active']

plt.figure(dpi=150)
plt.plot(monthly['date'], monthly['return'].cumsum(), label='passive')
plt.plot(monthly['date'], monthly['active'].cumsum(), label='volitility-managed')
plt.legend()
plt.xlabel('date')
plt.ylabel('cumulative returns')

Several studies have examined the economic value of volatility timing and found that it can add value to a portfolio. One study [1] measured the value of volatility timing as the estimated fee that a risk-averse investor would be willing to pay to switch from the ex-ante optimal portfolio to a volatility-timed portfolio. The study found that the value of volatility timing is positive and significant, indicating that it can improve the performance of a portfolio. Another study [2] considered two utility-maximizing volatility timing strategies based on maximizing the conditional expectation of benefits. The study found that both strategies can generate significant utility gains relative to a buy-and-hold strategy, indicating that volatility timing can be a profitable investment strategy. Another study [3] employs advanced statistical and machine learning methods to predict stock market volatility and utilizes these predictions for asset allocation and portfolio construction. It suggests that high-dimensional models, with a focus on the LASSO model, provide superior forecasts of market volatility, leading to enhanced investment performance, particularly when adjusting portfolios based on volatility timing. The study's findings have implications for investors and portfolio managers seeking to improve risk-adjusted returns in their investment strategies. However, some experts argue that timing the market is impossible [4]. They argue that trying to time the market based on volatility is a costly mistake and that investors should focus on long-term investment strategies instead of trying to predict short-term market movements. 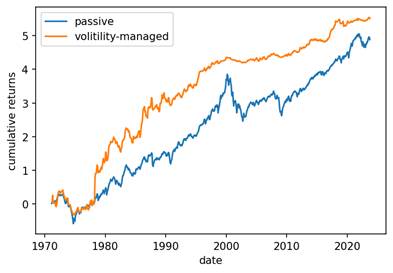In conclusion, volatility timing is an investment strategy that aims to adjust the exposure of a portfolio based on the volatility of the market. It involves calculating the standard deviation of the market returns, calculating the active return of the stock, standardizing the active return, and plotting the passive and active returns cumulatively over time. While some studies suggest that it can add value to a portfolio, others argue that it is impossible to time the market and that investors should focus on long-term investment strategies.