---

Expected Shortfall: Magnitude of Future Losses

---

VaR is lacking in the sense that it only deals with the percentage of losses not their value. So, we need a risk measure to give us the magnitude of large losses as well as their probability. Expected Shortfall (ES) or TailVar defined as below, gives us the expected value of future loss conditional on being worse than VaR:

 

The distribution tail gives us information on the range of possible extreme losses and the probability associated with each outcome. The Expected Shortfall aggregates this information into a single number by computing the average of the tail outcomes weighted by their probabilities.

Python Implementation

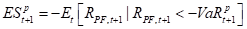
# import libraries
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# download price history
AAPL = yf.download('AAPL', start='2022-01-01').Close
plt.figure()
AAPL.plot()

# calculate returns
rets = np.log(AAPL/AAPL.shift(1))
rets.dropna(inplace=True)
plt.figure()
rets.plot()

plt.figure()
plt.hist(rets,50)

# fit normal distribution
mu, std = norm.fit(rets) 
x = np.linspace(-1, 1, 100)
p = norm.pdf(x, mu, std)
 
plt.plot(x, p, 'k', linewidth=2)

# calculate next day VaR and ES
h = 1
alpha = 0.01
CVaR = alpha**-1 * norm.pdf(norm.ppf(alpha))*std - mu
VaR = norm.ppf(1-alpha)*std - mu

print('VaR = %2.2f %%'%(VaR*100))
print('ES = %2.2f %%'%(CVaR*100))